机器学习全篇笔记

机器学习全篇笔记
BruceLee在整理近期的学习笔记时,我把机器学习入门阶段最常被问到的几个模块重新梳理了一遍:从逻辑回归的概率建模,到激活函数为何能让网络“弯起来”;从梯度下降的优化逻辑,到成本函数与正则化之间的取舍;再到数据集划分、偏差方差调试,以及最后的迁移学习实践。希望这篇文章能成为你快速复盘和查缺补漏的随身卡片。
一、逻辑回归
逻辑回归(Logistic Regression)是一种用于解决二分类问题的经典机器学习算法,其核心思想是通过线性模型结合 Sigmoid 函数,将线性输出映射到 0 到 1 之间的概率值,从而实现对样本类别的概率预测【1†source】。尽管名称中包含“回归”,但它实际上是一种分类算法。
1.核心原理
线性模型:
逻辑回归首先计算输入特征((X))与权重((W))的线性组合:
[ z = W^T X + b ]
其中 (b) 为偏置项。Sigmoid 函数:
通过 Sigmoid 函数将线性输出 (z) 映射到概率区间 ([0, 1]):
sigma(z) = 1 / (1 + e^(-z))输出值表示样本属于正类的概率(例如 (P(y=1|X)))。
决策边界:
通常以 0.5 为阈值:- 若 sigma(z) >= 0.5,预测为正类(1);
- 若 sigma(z) <= 0.5,预测为负类(0)。
2.训练与损失函数
损失函数:使用交叉熵损失(Log Loss)衡量预测概率与真实标签的差异:
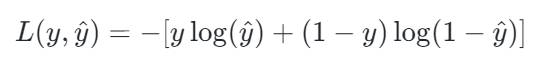
其中 (y) 为真实标签(0 或 1),(\hat{y}) 为预测概率。
参数优化:
通过梯度下降等优化算法最小化损失函数,更新权重 (W) 和偏置 (b)。
3.特点与适用场景
优点:
- 计算高效,可解释性强(权重反映特征重要性);
- 输出为概率,支持不确定性评估;
- 适用于线性可分或近似线性可分的数据。
局限性:
- 无法直接处理非线性决策边界(需结合特征工程或核方法);
- 对特征多重共线性敏感。
4.扩展应用
- 多分类问题:可通过 Softmax 函数推广到多分类(Multinomial Logistic Regression)【1†source】。
- 在金融风控、医疗诊断、广告点击率预测等领域广泛应用。
逻辑回归是机器学习入门的基础模型,理解其原理有助于深入学习更复杂的算法(如神经网络)。
二、激活函数
1.神经网络为什么需要激活函数?
神经网络需要激活函数,核心原因是为网络引入非线性能力,否则无论网络有多少层,最终都只是线性变换,无法拟合现实世界中复杂的非线性问题。
具体作用可分为三点:
引入非线性:现实中的数据关系(如图像识别、语音处理中的特征映射)大多是非线性的。激活函数(如ReLU、Sigmoid)通过非线性变换,让神经网络能学习并表示这些复杂关系,例如区分不同形状的物体、识别不同语调的语音。
控制梯度流动:合理的激活函数(如ReLU)能缓解“梯度消失/爆炸”问题。例如ReLU在正区间的梯度恒为1,可让深层网络的梯度有效传递,保证模型能正常训练;而早期的Sigmoid函数因两端梯度趋近于0,容易导致深层网络训练停滞。
调整输出特征分布:激活函数能将神经元的输出值映射到特定范围(如Sigmoid映射到[0,1]、Tanh映射到[-1,1]),使特征分布更稳定,避免因数值过大或过小导致网络训练波动,同时也能为后续层的计算提供更合适的输入特征。
2.激活函数:神经网络的非线性引擎
为什么必须使用非线性激活函数?
数学证明:线性网络的局限性
假设一个L层神经网络,每层使用线性激活函数:
𝑓(𝑥)=𝑊𝐿(𝑊𝐿−1(⋯(𝑊2(𝑊1𝑥+𝑏1)+𝑏2)⋯)+𝑏𝐿−1)+𝑏𝐿
这可以简化为:
𝑓(𝑥)=𝑊′𝑥+𝑏′
结论:无论网络多深,线性激活函数都会使整个网络退化为单层线性模型,无法学习复杂非线性关系。
非线性变换的重要性
特征学习:通过非线性组合,网络可以学习数据的层次化特征表示
万能近似定理:单隐藏层神经网络配合非线性激活函数可以近似任何连续函数
决策边界:非线性激活函数使网络能够学习复杂的非线性决策边界
3.三个常见的激活函数

线性激活函数不能用于隐藏层,因为它会将线性一直传递下去,导致输出层输出的还是线性函数
ReLu一般用于隐藏层,因为其大于0是,梯度恒为1,可保证模型正常训练
三、梯度下降
梯度下降(Gradient Descent)是一种广泛应用于机器学习和深度学习中的优化算法,其核心目标是通过迭代调整模型参数,最小化损失函数(或目标函数)的值。以下从原理、算法步骤、关键组件、变种及优缺点等方面详细介绍。
1.核心原理
梯度下降基于函数的梯度(Gradient)方向进行优化。梯度是一个向量,表示函数在某一点对各参数偏导数的集合,指向函数值上升最快的方向。因此,负梯度方向即为函数值下降最快的方向。算法通过沿负梯度方向逐步更新参数,使损失函数值逐渐减小,最终收敛到局部最小值或全局最小值(若函数为凸函数)。
其数学原理可通过泰勒展开近似解释:

2.算法步骤
- 初始化参数:随机选择初始参数值(如全零或随机值)。
- 计算梯度:计算当前参数下损失函数的梯度(即偏导数)。
- 更新参数:沿负梯度方向调整参数。
- 重复迭代:重复步骤2-3,直到梯度接近零或达到预设迭代次数。
3.关键组件
学习率(Learning Rate, alpha):
- 控制参数更新的步长。学习率过大会导致震荡或无法收敛;过小则收敛速度慢。
- 需根据问题调整,也可采用自适应学习率策略(如Adam、RMSprop)。
损失函数(Loss Function):
- 用于衡量模型预测值与真实值的误差,如均方误差(MSE)、交叉熵(Cross-Entropy)。
- 梯度下降的目标是最小化该函数。
4.主要变种算法
梯度下降的经典变种包括:
批量梯度下降(BGD):
- 每次迭代使用全部训练数据计算梯度,收敛稳定但计算开销大。
随机梯度下降(SGD):
- 每次随机使用一个样本计算梯度,收敛快但波动大。
小批量梯度下降(MBGD):
- 折中方案,使用小批量样本计算梯度,平衡效率与稳定性。
改进优化算法:
- Momentum:引入动量项加速收敛,减少震荡。
- AdaGrad:自适应调整学习率,适合稀疏数据。
- RMSprop:改进AdaGrad,避免学习率过早衰减。
- Adam:结合Momentum和RMSprop的优点,自适应调整学习率和动量,广泛应用于深度学习。
5.优缺点
优点:
- 通用性强,适用于多种模型(如线性回归、神经网络)。
- 实现简单,计算效率高(尤其变种算法如SGD、Adam)。
缺点:
- 可能收敛到局部最小值(非凸函数中)。
- 学习率选择敏感,需调参。
- 对高维或稀疏数据可能收敛慢。
6.应用场景
梯度下降是机器学习的核心优化工具,常用于:
- 神经网络训练(如CNN、RNN)。
- 线性回归、逻辑回归的参数求解。
- 深度学习框架(如PyTorch、TensorFlow)中的优化器实现。
总结
梯度下降通过迭代和梯度信息高效优化模型参数,其变种算法(如Adam)进一步提升了收敛速度和稳定性。理解其原理及组件(如学习率、损失函数)对机器学习实践至关重要。实际应用中需根据数据特性选择合适的变种算法,并合理调参以达到最佳效果。
四、成本函数,损失函数及其正则化
1.区别与联系
首先,需要理解这两个密切相关但略有区别的概念。
损失函数 (Loss Function),又称误差函数 (Error Function)
- 定义:衡量单个训练样本的预测值 与真实值之间的差异或“损失”的函数。它计算的是单个点的误差。
- 目的:指导模型如何根据一个样本调整其参数以减少误差。
- 常见类型:
- **均方误差 (MSE - Mean Squared Error)**:主要用于回归问题。损失值为预测值与真实值之差的平方。
- **交叉熵损失 (Cross-Entropy Loss)**:主要用于分类问题。衡量预测概率分布与真实概率分布之间的差异。
成本函数 (Cost Function),又称目标函数 (Objective Function)
定义:衡量整个训练集上所有样本的预测值与真实值之间的平均差异。它是所有样本损失函数的平均值。
目的:作为模型训练的整体优化目标。机器学习算法的核心就是找到一组参数 alpha,使得成本函数 J(alpha) 的值最小化。
成本函数是损失函数在整个数据集上的聚合。
简单比喻:
- 损失函数:就像你一次考试中做错一道题扣的分数。
- 成本函数:就像你整个学期所有考试的平均分。你的目标是让这个平均分(成本函数)越高(对应误差越低)越好。
2.线性回归的平方误差成本函数
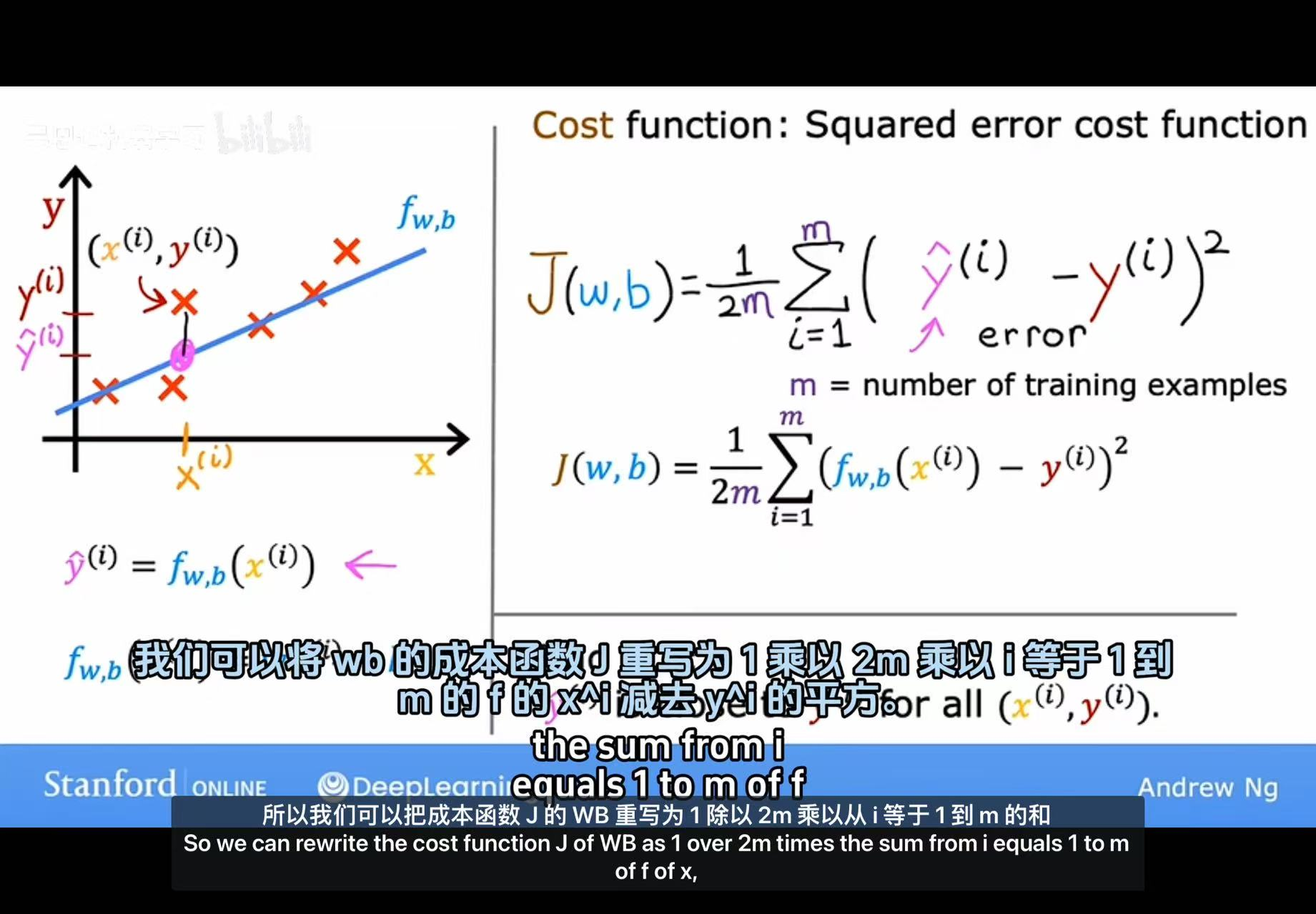
• 核心含义:用于线性回归任务(预测连续值,如房价、气温),衡量模型预测值与真实值的“平方误差”。
• 公式解释:
◦ m 是训练样本数量;
◦ 除以 2m 是为了后续求导时简化计算(导数中的系数会抵消)。
• 直观理解:左边的坐标系中,蓝色直线是模型预测的直线,红色“×”是真实数据点,误差是“真实点到直线的垂直距离的平方和”,损失函数的目标是最小化这个平方和,让直线尽可能拟合所有数据点。
3.逻辑回归的交叉熵成本函数
(1)分段形式

(2)简洁形式

3. 正则化 (Regularization)
为什么要正则化?
当模型过于复杂(参数过多或权重过大)时,它可能会过度拟合(Overfitting)训练数据。这意味着它在训练集上表现非常好,但遇到未见过的测试数据时表现很差,泛化能力弱。正则化是一种用于防止过拟合的技术。
核心思想
在成本函数中额外添加一个“惩罚项”(Penalty Term),这个惩罚项与模型参数的复杂度(通常是权重的大小)成正比。这样,在最小化成本函数的过程中,算法不仅要去拟合数据,还要尽量保持参数的值较小,从而约束模型的复杂度,使其变得更简单、更平滑。
常见的正则化方法
(1)L2 正则化 (L2 Regularization) / 岭回归 (Ridge Regression)
- 惩罚项:所有权重参数的平方和。
- 效果:倾向于让权重参数趋向于0,但不会完全变为0(除非必要)。它使模型的所有特征都保留一点贡献,但削弱不重要特征的影响。这使得解更稳定。
- 公式:正则化后的成本函数为:

- lambda:正则化参数,是一个超参数,控制惩罚的强度。$\lambda$ 越大,惩罚越重,模型越简单。
- 1/2m:是为了方便求导后的计算,有时也会省略。
(2)L1 正则化 (L1 Regularization) / 套索回归 (Lasso Regression)
惩罚项:所有权重参数的绝对值之和。
效果:倾向于让一部分不重要的特征的权重直接变为0。因此,L1正则化天然具备特征选择(Feature Selection) 的能力,可以产生稀疏的模型。
公式:
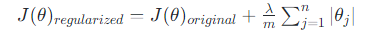
(3)弹性网络正则化 (Elastic Net)
惩罚项:L1正则化和L2正则化的结合。
效果:结合了L1和L2的优点,既能进行特征选择,又能保持模型的稳定性。通常在特征高度相关时使用。
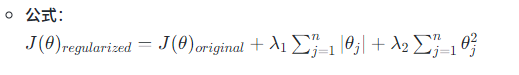
正则化代码

4.总结与关系
| 概念 | 作用层级 | 目的 | 示例 |
|---|---|---|---|
| 损失函数 (Loss) | 单个样本 | 计算单个预测的误差 | MSE, Cross-Entropy |
| 成本函数 (Cost) | 整个数据集 | 衡量模型整体误差,作为优化目标 | $J(\theta) = \frac{1}{m}\sum L$ |
| 正则化 (Regularization) | 成本函数 | 在成本函数中添加惩罚项,防止过拟合 | L1正则化, L2正则化 |
最终,一个完整的、带有正则化的机器学习模型的目标是:
最小化正则化后的成本函数:
其中 R(theta)是正则化项(如 L1 或 L2 范数)。通过调整超参数 lambda,我们可以在“拟合训练数据”和“保持模型简单”之间找到最佳平衡。
Sigmoid函数和Softmax函数都是机器学习中常用的激活函数,主要用于将模型的原始输出转换为概率分布,但它们在应用场景和数学特性上存在显著差异。
五、Sigmoid函数与 Softmax函数
1.Sigmoid函数
Sigmoid函数(也称为逻辑函数)是一种S型曲线函数,其数学表达式为:
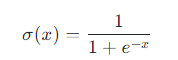
该函数将任意实数输入映射到(0,1)区间内,具有以下特性:
输出范围:(0,1),适合表示概率。
连续性:函数处处连续且光滑,便于求导。
对称性:关于点(0,0.5)中心对称。
导数特性:其导数可以用自身表示,即
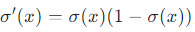
,计算高效。
应用场景:
- 二分类问题:常用于逻辑回归或神经网络的输出层,将输出解释为样本属于正类的概率[[4]][[5]]。
- 阈值函数:在神经网络中作为激活函数,引入非线性(但现代深度学习较少使用,因存在梯度消失问题)。
- 其他领域:如心理学中的学习曲线建模、热传导问题及岩土工程中的土压力计算[[6]][[7]]。
优缺点:
- 优点:输出概率意义明确、求导简单。
- 缺点:易导致梯度消失(输入值极大或极小时梯度接近零)、输出非零中心(可能影响训练效率)。
2.Softmax函数
Softmax函数是Sigmoid函数在多分类问题中的推广,其数学表达式为:
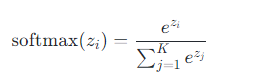
其中 (z = (z_1, z_2, …, z_K)) 是一个K维向量。该函数将任意实数向量转换为概率分布,具有以下特性:
- 输出性质:所有输出值在(0,1)范围内,且总和为1,符合概率公理。
- 单调性:输入值 (z_i) 增大时,对应输出概率增加。
- 数值稳定性:可通过减去输入向量中的最大值(即 (z_i - max(z)))避免计算指数时溢出。
应用场景:
- 多分类问题:广泛用于神经网络的输出层(如图像分类、自然语言处理),将原始输出转换为各类别的概率分布。
- 与交叉熵损失结合:作为损失函数的一部分,优化模型预测与真实标签的差异。
优缺点:
- 优点:输出为概率分布,直观且适用于多类别场景;与交叉熵损失配合时梯度计算高效。
- 缺点:计算复杂度较高(需计算所有元素的指数和);可能因指数函数导致数值不稳定(需通过优化技巧避免)。
3.关键区别
- 输出维度:
- Sigmoid:标量输出,适用于二分类。
- Softmax:向量输出,适用于多分类(K≥2)。
- 概率和:
- Sigmoid:单个输出值表示概率,但多个Sigmoid输出的总和不一定为1。
- Softmax:所有输出值之和严格为1,形成概率分布。
- 数学关系:当K=2时,Softmax可退化为Sigmoid,但两者在实现和解释上通常区别处理[[14]][[15]]。
4.选择建议
- 使用Sigmoid:当问题为二分类或需对多个二分类任务独立输出概率时(如多标签分类)。
- 使用Softmax:当问题为互斥多分类(每个样本仅属一个类别)且需概率分布时。
两者均为深度学习中的基础组件,实际选择需结合具体任务和模型结构。


5.代码实现
基础形式
改进形式

改进原因
这是在讲解数值精度优化,核心是通过调整模型的损失函数和激活函数实现更准确的计算,避免“数值舍入误差”。
1. 逻辑回归的改进逻辑
在逻辑回归中,原本的损失函数依赖sigmoid输出的概率 a (即 a = 1/(1 + e ^ (-z)))。但直接计算 a 时,若 z 过大或过小,容易出现数值溢出(比如 e^(-z) 趋近于0或无穷大)。
改进方法是绕过中间概率 a ,直接用原始得分 z 计算损失,

让框架直接基于原始得分 z 计算损失,避免中间步骤的精度丢失。
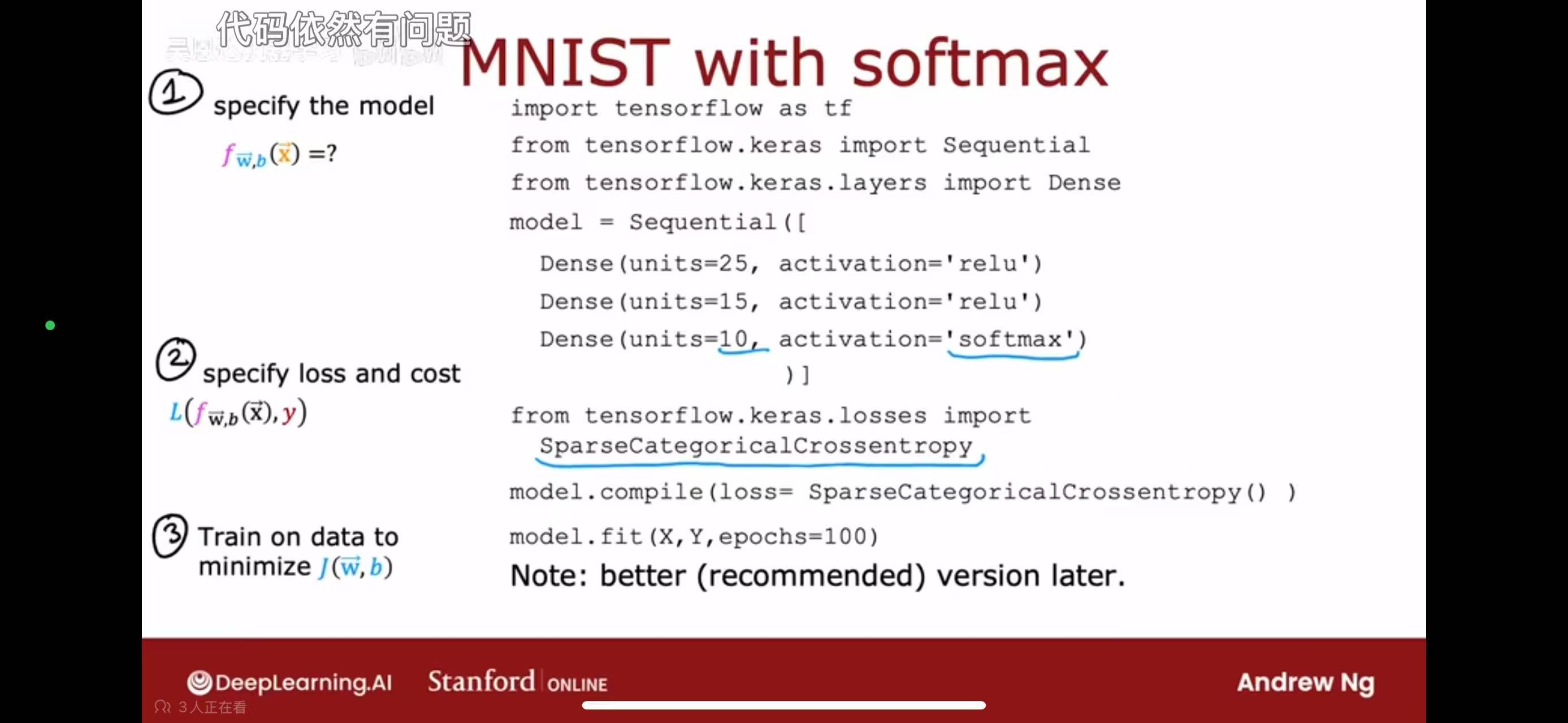
2. Softmax回归(以MNIST为例)的改进逻辑
在多分类任务中,原本的模型最后一层用softmax激活函数输出概率。但同样存在数值溢出问题( e^(z_j) 可能因 z_j 过大而溢出)。
改进方法是最后一层用线性激活(linear)输出原始得分 z_j ,再在损失函数中集成Softmax计算。代码中通过设置 from_logits=True,让损失函数(如SparseCategoricalCrossentropy)内部同时完成“Softmax概率转换 + 交叉熵损失计算”,这样可以利用框架的数值稳定优化(比如先对 z_j 做归一化再计算指数),避免直接计算softmax时的精度问题。
总结来说,这种改进的核心是跳过中间概率的显式计算,直接基于模型的原始得分(logits)计算损失,从而避免数值舍入或溢出带来的精度误差,让模型训练更稳定、结果更准确。
3.关于原本的损失函数sigmoid化简后为什么不会出现下溢

六、训练集,验证集以及测试集
在机器学习中,数据集通常被划分为训练集、验证集和测试集,三者分工明确,共同确保模型的可靠性和泛化能力。
1.训练集(Training Set)
训练集是模型学习的基础数据,用于拟合模型参数(如神经网络中的权重和偏置)。通过反复迭代训练,模型从训练集中学习数据的内在规律和特征,逐步优化其预测能力。
2.验证集(Validation Set)
验证集用于模型调优和超参数选择(如学习率、网络层数等)。在训练过程中,通过验证集评估不同超参数组合下模型的性能,防止过拟合(即模型过度适应训练数据而丧失泛化能力),并辅助决策(如早停法)。其核心作用是提供“模拟考试”环境,避免测试集被间接泄露到训练环节。
3.测试集(Test Set)
测试集是模型训练完成后的最终评估数据,用于无偏评估模型的泛化性能。它模拟真实场景中的未知数据,检验模型是否具备实际应用价值。测试集必须严格独立于训练和验证过程,且仅使用一次。
4.为何需要验证集?
引入验证集的主要原因包括:
- 超参数优化:超参数(如正则化强度、迭代次数)无法通过训练集学习,需依赖验证集进行调优。
- 防止过拟合:仅依赖训练误差选择模型可能导致过拟合,验证集提供中间评估,帮助识别泛化能力最佳的模型。
- 保护测试集独立性:若直接使用测试集调参,会导致模型间接“窥见”测试数据,使最终评估结果失真。

• 若直接用测试集评估不同次数的多项式模型(如d=1,2,…,10),再选测试误差最小的d,会导致测试集误差过于乐观(因为模型在测试集上“作弊”了)。
• 解决方法:引入验证集(Validation Set),先用训练集训练不同模型,再用验证集选最优模型,最后用测试集评估泛化能力。
5.三者的成本函数(只有训练集需要正则化)

6.只有训练集需要正则化的原因
要理解“只有训练集需要正则化”,需从正则化的目的和模型评估的逻辑两方面分析:
1. 正则化的核心目的
正则化(如L2正则化)是为了约束模型复杂度,防止训练集上的过拟合。它通过给权重w添加惩罚项,迫使模型“不要过于依赖某几个特征”,从而提升泛化能力。
这个操作是训练阶段的“约束手段”,只有在训练时需要——因为训练的目标是“让模型在学到数据规律的同时,不要学太多噪声”。
2. 测试/验证阶段的逻辑
当模型训练完成后,我们需要评估它在 unseen 数据(测试集/验证集)上的泛化能力。此时:
• 测试/验证集的作用是模拟真实场景,要反映模型“不加约束时的预测能力”。
• 若在测试阶段也加入正则化,相当于“人为给模型加了额外约束”,会导致测试误差不能真实反映模型的泛化能力(比如正则化可能让测试误差看起来更小,但这是虚假的)。
举个例子
假设你训练了一个“带正则化的复杂模型”,在测试时如果继续加正则化,就像“考试时还在强制自己‘不能写太复杂的步骤’”——这不是真实的考试能力,而是额外约束下的表现。因此,只有训练集需要正则化,测试/验证阶段只需评估模型的原始预测能力。
七、模型调试(方差与偏差)
在机器学习中,高偏差(High Bias)和高方差(High Variance)是模型泛化误差的两个核心来源,反映了模型在训练和预测过程中的不同问题。以下是详细分析:
1、高偏差(High Bias)–> 欠拟合
定义与表现
高偏差指模型过于简单,无法捕捉数据中的复杂模式,导致预测结果系统性偏离真实值。典型表现为:
- 训练误差和测试误差均较高,且两者差距较小;
- 模型欠拟合(Underfitting),即对训练数据的拟合不足。
常见原因
- 模型复杂度不足(如使用线性模型拟合非线性关系);
- 特征工程不充分(缺少关键特征或未构造有效特征)。
解决策略
- 增加模型复杂度(如使用更高阶多项式、更深的神经网络);
- 引入更多特征或构造新特征;
- 减少正则化强度(如降低正则化参数λ)。
2、高方差(High Variance)–> 过拟合
定义与表现
高方差指模型过度拟合训练数据中的噪声或细节,导致泛化能力差[[9]]。典型表现为:
- 训练误差低,但测试误差高,两者差距大;
- 模型过拟合(Overfitting),对训练数据过度敏感。
常见原因
- 模型过于复杂(如高阶多项式、未正则化的深度网络);
- 训练数据量不足或噪声过多[[14]]。
解决策略
增加训练数据量;
降低模型复杂度(如减少特征数量、简化网络结构);
增强正则化(如增大L2正则化参数λ、使用Dropout);
采用集成方法(如Bagging)降低方差。

3、偏差-方差权衡(Bias-Variance Tradeoff)
理想模型需平衡偏差和方差,以达到低总误差(误差 = 偏差² + 方差 + 不可约误差)。
- 低偏差低方差:模型既准确又稳定(如合理正则化的深度网络);
- 高偏差低方差:预测稳定但系统性偏离(如欠拟合的线性模型);
- 低偏差高方差:预测准确但不稳定(如过拟合的复杂模型)。
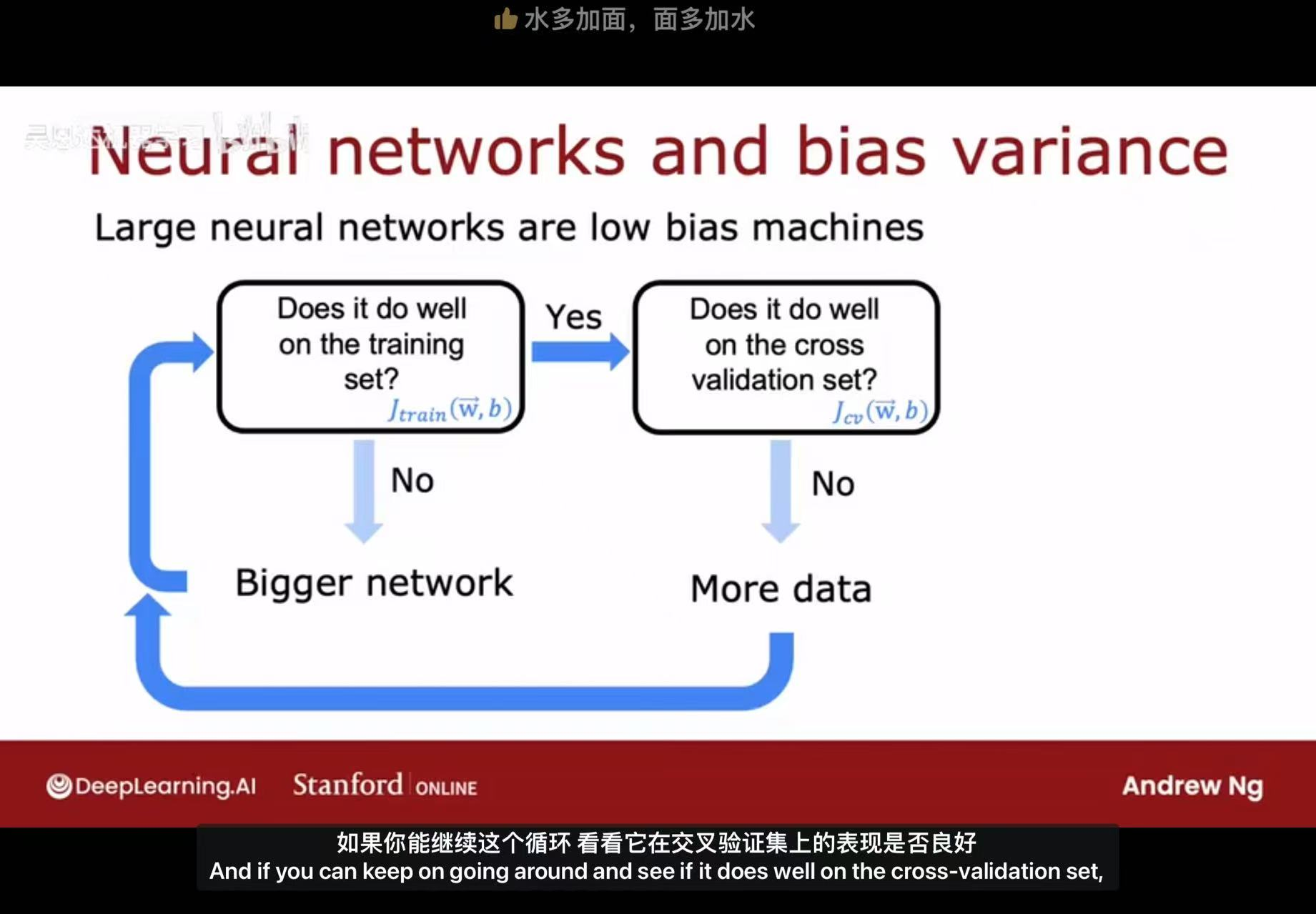
4、实际判断与调整
通过学习曲线可直观诊断:
- 若训练误差和验证误差均高且接近 → 高偏差;
- 若训练误差低但验证误差高 → 高方差。
调整方向:
高偏差需提升模型能力,高方差需增强泛化性。
5、示例说明
- 高偏差案例:用线性回归拟合二次函数数据,误差始终较大;
- 高方差案例:用高阶多项式回归拟合少量数据,训练误差近乎零但测试误差骤增。
理解并平衡偏差与方差是优化模型性能的关键,需根据具体问题动态调整模型复杂度与正则化策略。
八、迁移学习
为什么要进行迁移学习?
进行迁移学习主要源于以下几个关键原因:
(1) 解决数据稀缺问题
很多实际任务中,我们能获取的标注数据非常少(比如医疗影像、小众领域的图像/文本分类)。而迁移学习可以利用在大型通用数据集(如ImageNet、维基百科文本)上预训练好的模型,将其学到的通用特征(如“边缘、纹理”“语法、语义”)迁移到新任务中,无需从零开始训练,大幅降低对自有数据量的依赖。
(2) 降低训练成本
训练一个深度神经网络(如ResNet、BERT)需要大量的计算资源和时间。迁移学习直接复用预训练模型的参数,只需“微调”少量层即可适配新任务,能节省算力、缩短训练周期(比如原本需要几天的训练,迁移学习可能几小时就能完成)。
(3) 提升模型泛化能力
预训练模型在大型数据集上学习到的是通用且鲁棒的特征表示(比如图像中的“形状抽象”、文本中的“语义逻辑”)。将这些特征迁移到新任务后,模型能更好地应对新数据中的变化(如不同的拍摄角度、不同的表达方式),从而提升泛化能力。
(4) 适配小众任务
对于一些小众或专业领域的任务(如“识别特定工业零件缺陷”“分析某领域学术论文情感”),很难收集到足够的标注数据来训练专属模型。迁移学习可以让模型先在通用领域“打好基础”,再快速适配这些小众场景。
举个例子:要做“识别不同品种的兰花”的图像分类任务,直接训练的话,自己的兰花数据可能只有几百张,模型容易过拟合。但如果先下载在ImageNet(含数百万张各类图像)上预训练好的模型,再用自己的兰花数据微调,模型就能快速学会“兰花的花瓣形状、纹理”等特征,效果远好于从零训练。
如何进行迁移学习
迁移学习(Transfer Learning)是一种让模型“借力已有知识”来解决新任务的机器学习方法,步骤如下:
• 步骤1:下载(或自行训练)一个在大型数据集上预训练好的神经网络参数。这个数据集的输入类型要和你的应用场景一致(比如都是图像、音频或文本)。例如,如果你要做“猫/狗分类”的图像任务,可以下载在ImageNet(大型图像数据集)上预训练好的ResNet、VGG等模型的参数。
• 步骤2:用你自己的小数据集对这个预训练网络进行微调(fine tune),让它适配你的具体任务。
简单来说,迁移学习就是“先借别人在大数据上学到的通用知识,再用自己的小数据把知识掰成适合自己任务的形状”,能有效解决小数据场景下的模型训练问题。